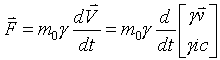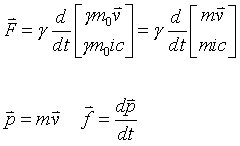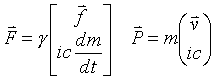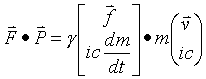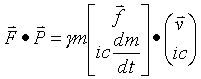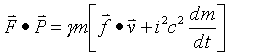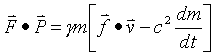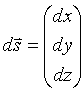
Define three space displacement

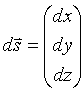
Assume two frames of reference. One is at rest and the second frame of reference is moving at the speed (ν). The speed of light (c) is constant and must be the same in both frames of reference. Define four space displacement with respect to the, at rest, inertial frame time (t) and proper time (τ) measured in the moving frame

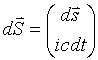
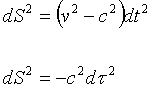
Define three space velocity of the moving frame of reference

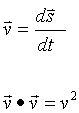
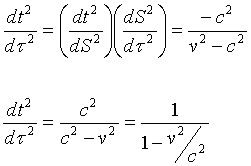
Now the Lorentz factor (γ) falls out as the ratio of (dt) to (dτ)

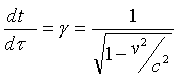
Find 4-Force in terms of 3-space variables:

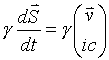
Now four space velocity

Now four space momtum

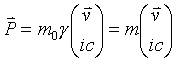
Now four space force

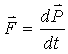
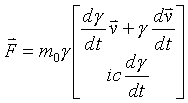
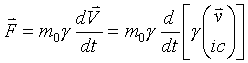
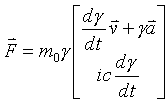
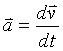
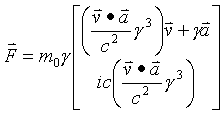
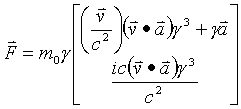
Now starting with the relativistic scalar correction factor

gamma

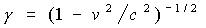
Next the time derivative of gamma 

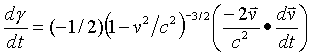
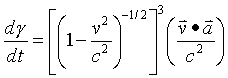
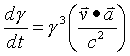
Now find the vector dot product of F and P

(or the scalar product

of 4-force and 4-momentum)

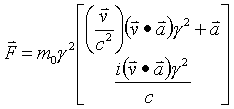
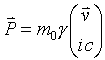
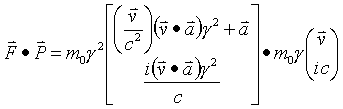
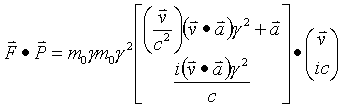
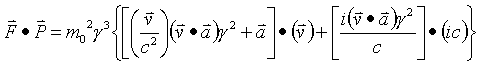
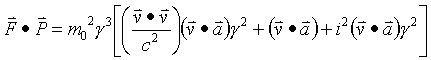
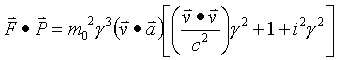
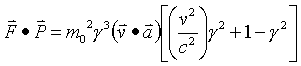
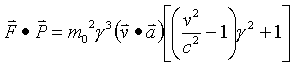
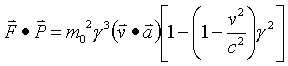
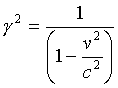
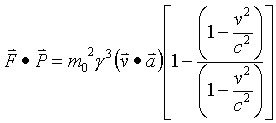
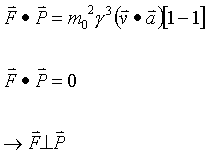
Therefore the 4-force and 4-momentum acting on objects with rest mass are always perpendicular.

Now relate the four dimensional force and momentum dot product to three dimensional force and momentum.